Sine and cosine are very nice functions, aren't they? Many simple 2D effects such as scrollers or wobblers are based on them, and they are vital for any 3D engine (e.g. they are used in the rotation functions). But have you ever wondered how these functions (and others, such as tan, log, exp, sqr) are actually implemented in your computer? If you programmed in Assembler before the FPU became common in computers, you certainly did and probably already learned about the underlying method - Taylor polynoms. But if you're a comparatively young coder, this article may be of interest for you.
Requirements: You need some knowledge of calculus to understand how Taylor polynoms work.
For starters: How trigonometric functions work
In a right-angled triangle, the sine of an angle is the quotient of its opposite side divided by the hypotenuse. The cosine of this angle is the quotient of its adjacent side divided by the hypotenuse.
There's a simple geometrical way to calculate the sine and the cosine of any angle: Draw a two-dimensional system of coordinates and a circle with center (0, 0) and the radius 1. The right part of the horizontal line indicates the 0-degree-mark. Using an ordinary geometry set square, draw a line with the desired angle between it and the 0-degree-mark (note: angles are always measured in counter-clockwise order!). Now have a look at the intersection point: Its x-coordinate is the cosine of the angle, and its y-coordinate is the sine of the angle.
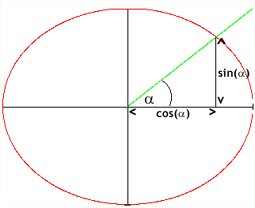
All right, this is easy for a human being who has the required tools and abilities. But what about a computer, this simple calculating device? It can't draw and thus derive a value. There's only sort of functions a computer can easily process: polynom functions. A polynom function is a function of the following form:

The value n is called "order of the polynom".
So what we have to do is to transform the trigonometric functions to polynom functions.
Approximating non-polynom functions by polynoms
First of all, it is not possible to transform periodic functions such as sine and cosine of which you can compute an infinite number of derivations to polynom functions of finite order in such a way that the resulting polynom functions exactly produce the same values for all parameters as the original non-polynom functions. It is only possible to compute polynom functions that approximately match the original ones. Usually the following rule applies: The higher the order of the polynom function, the better the approximation.
A rather simple method to approximate a function f(x) in a certain range by a polynom P_n of n-th order is to take n+1 parameters x_i in this range for which we know f(x_i). Inserting these values in the general formula of P_n, we get a system of equations which we can solve using matrices or other methods.
Example:
We want to transform f(x)=cos(x) to a polynom P_2 of 2nd order in the range of 0 to 180 degrees (i.e., in radiants, 0 to pi). We know that cos(0)=1, cos(pi/2)=0 and cos(pi)=-1. We get the following equations:
1 = a_2 * 0^2 + a_1 * 0 + a_0 (I)
0 = a_2 * (pi/2)^2 + a_1 * (pi/2) + a_0 (II)
-1 = a_2 * pi^2 + a_1 * pi + a_0 (III)
(I) shows: a_0 = 1. Inserting this into equations (II) and (III), we get:
-1 = a_2 * (pi/2)^2 + a_1 * (pi/2) (IV)
-2 = a_2 * pi^2 + a_1 * pi (V)
(V) - 2 * (IV) results in:
-2 + 2 = a_2 * pi^2 - 2 * a_2 * (pi/2)^2 + a_1 * pi - 2 * a_1 * (pi/2) =>
=> 0 = a_2 * pi^2 - a_2 * pi^2 / 2 =>
=> 0 = a_2 * pi^2 / 2 =>
=> a_2 = 0 (VI)
By inserting this into (V) we can finally compute a_1:
-2 = a_1 * pi =>
=> -2/pi = a_1
The resulting polynom function is:
P_2(x) = -2/pi * x + 1
This was already quite a lot of work, and it's a very bad approximation: Only for the defined values 0, pi/2 and pi does P_2(x) match f(x). For the other values in this range, it gives a very rough approximation - and, even worse: for all values outside this range, it produces utter nonsense! Look at these graphs drawn by MathCAD:
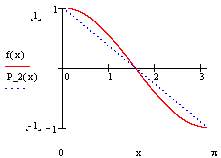
Calculating a polynom of a higher order (which I leave to you as an exercise) only increases the number of parameters for which the polynom function matches the original function but the basic problems remain the same. Moreover, the higher the order of the polynom, the harder and more time-consuming it is to compute.
There has to be a better way to approximate a function using a polynom. And there is one.
Taylor polynoms
Let's have a look at a polynom function of 3rd order:
f(x) = a_3 * x^3 + a_2 * x^2 + a_1 * x + a_0
We can compute up to 3 derivations of this function:
f'(x) = 3 * a_3 * x^2 + 2 * a_2 * x + a_1
f''(x) = 6 * a_3 * x + 2 * a_2
f'''(x) = 6 * a_3
Now suppose we know the value of P_3(x_0) and want to compute P_3(x), where x = x_0 + h. We get:
f(x_0 + h) = a_3 * (x_0 + h)^3 +
a_2 * (x_0 + h)^2 +
a_1 * (x_0 + h) +
a_0 =
= a_3 * (x_0^3 + 3 * x_0^2 * h + 3 * x_0 * h^2 + h^3) +
a_2 * (x_0^2 + 2 * x_0 * h + h^2) +
a_1 * (x_0 + h) +
a_0 =
= (a_3 * x_0^3 + a_2 * x_0^2 + a_1 * x_0) +
h * (3 * a_3 * x_0^2 + 2 * a_2 * x_0 + a_1) +
h^2 * (3 * a_3 * x_0 + a_2) +
h^3 * a_3 =
= f(x_0) +
h * f'(x_0) +
1/2 * h^2 * f''(x_0) +
1/6 * h^3 * f'''(x_0) =
= 1/0! * h^0 * f(x_0) +
1/1! * h^1 * f'(x_0) +
1/2! * h^2 * f''(x_0) +
1/3! * h^3 * f'''(x_0)
Wow! Isn't this cute? And now let me tell you,
a) that this not only works with a polynom function of 3rd order, but with any order - e.g. for a polynom function of 4th order, we'd just have to add 1/4! * h^4 * f''''(x_0),
b) that this not only works with a polynom function but with any function, and thus it can be used in order to transform a non-polynom function to a polynom function. However, this requires that we must be able to compute all its derivations. Since sine and cosine are periodic functions, the number of computable derivations is infinite. Thus we can only compute polynoms that approximately match the original functions.
Yet this is better than nothing, as this method of approximating non-polynom functions has a vast advantage in comparison to the method described in the previous section: It's easier to compute, and if we want to improve the approximation by generating a polynom of a higher order (e.g. 5 instead of 3), we just have to add the "missing links" (e.g. 1/4! * h^4 * f''''(fx_0) + 1/5! * h^5 * f'''''(x_0)) instead of calculating it all over again.
The general formula of these polynom functions - the "Taylor polynoms", named after their discoverer Brook Taylor (1685-1731) - is:
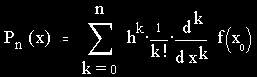
For approximating functions, most of the time x_0 := 0, h := x is used. (One of the exceptions is log(x), as log(0) doesn't exist.) We get a special form of Taylor's formula, the MacLaurin formula:
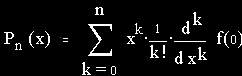
Example:
Let's use MacLaurin's formula to transform f(x)=cos(x) to a polynom of 6th order. First, we calculate the first six derivations of f(0):
f(x) = cos(x) => f(0) = 1
f'(x) = -sin(x) => f'(0) = 0
f''(x) = -cos(x) => f''(0) = -1
f'''(x) = sin(x) => f'''(0) = 0
f''''(x) = cos(x) => f''''(0) = 1
f'''''(x) = -sin(x) => f'''''(0) = 0
f''''''(x) = -cos(x) => f''''''(0) = -1
Second, we insert this into the formula:
P_6(x) = 1/0! * x^0 * 1 +
1/1! * x^1 * 0 +
1/2! * x^2 * (-1) +
1/3! * x^3 * 0 +
1/4! * x^4 * 1 +
1/5! * x^5 * 0 +
1/6! * x^6 * (-1) =
= 1 - 1/2 * x^2 + 1/24 * x^4 - 1/720 * x^6
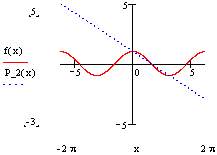
Finished! It's as simple as that. Below you see the result:
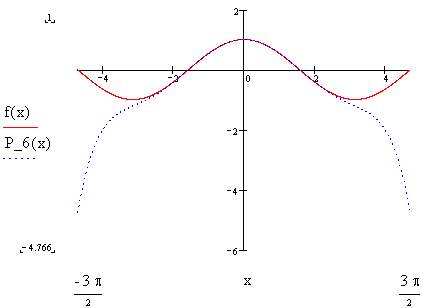
The approximation is pretty good in the area around x=0, but outside it it's as wrong as any polynom approximation generated by any other method. However, that's inevitable. After all, to get a perfect match, we'd need a polynom of infinite order, i.e. a series ("Taylor series").
Exercise:
Prove that the Taylor series of f(x)=cos(x) is:
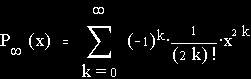
Implementation
Understanding Taylor's formula, you now know how the theory how to enable computers to process non-polynom functions such as sine, cosine, tangent, exponential functions and logarithm functions. Now comes the practical part - the implementation.
It's not so hard to get a function implemented now, but there are plenty of opportunities to optimize them. This is a creative task and thus a lot of fun.
A possible implementation of cosine in C is my following function:
typedef float radiants;
float cos(radiants angle, int precision)
{
float cosine = 1, xtag = 1, quangle = angle * angle;
int faculty = 1, i;
for(i = 1; i < precision; i++ )
{
faculty *= i;
i++;
faculty *= i;
faculty = ~faculty ++;
xtag *= quangle;
cosine += xtag / faculty;
}
return cosine;
}
This version already includes some tricks to gain a better performance. Yet it can be improved a lot. For example, it uses floating point variables. What about fixed-comma variables? They can be simulated using integers and usually run a lot faster, albeit they, of course, have lower precision.
Also mind that you usually do not want to calculate only one angle but several at a time. Quite a lot (depending on the chosen precision) of co-efficients are calculated every time the above function is executed. Why not calculate them once, store them in a table and then look 'em up? I leave this to you as an exercise. When you are finished, you can compare your solution with mine, which is located in the bonus pack.
And a final challenge: Can the function be changed to give approximately correct results for any angle, even if you only use a polynom of a finite order? The answer, of course, is: yes. Try to implement it. Hint: Take a close look (or several close looks) at the circle described in the first section of this article. My solution is included in the bonus pack as well.
There are also other ways of calculating sine and cosine. Franky explains some of them in his Sine Generation Tutorial in Hugi 16. These ones are especially useful if you want to generate a table of all sines/cosines of angles in a certain range with a fixed distance between them.
For any comments or suggestions feel free to mail me!